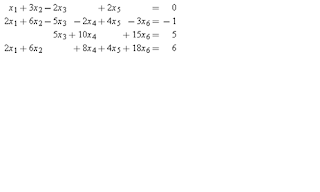METODE GAUSS SEIDEL

METODE GAUSS-JORDAN

Ide pada metoda eliminasi Gauss adalah mengubah

matriks ke dalam bentuk echelon-baris tereduksi.

CONTOH: Diberikan SPL berikut.

Bentuk matriks SPL ini adalah:

METODE GAUSS

Metode Gauss adalah suatu tahapan untuk memecahkan persamaan dengan cara mereduksi / menyederhanakan matriks persamaan tesebut. Prosedur dalam metode Gauss akan menghasilkan bentuk matriks pada eselon terreduksi

Teorema dalam metode Gauss :
 

Jika baris tidak terdiri seluruhnya dari nol, maka bilangan tak nol pertama

    dalam baris tersebut adalah 1. (di sebut 1 utama)

Jika terdapat baris yang seluruhnya terdiri nol, maka semua baris seperti itu

    dikelompokkan bersama-sama dibawah matriks

Dalam sebarang dua baris yang berturutan yang seluruhnya tidak terdiri dari

     nol, maka 1 utama dalam baris yang lebih rendah terdapat lebih jauh ke kanan

     dari 1 utama dalam baris yang lebih tinggi.

     Masing-masing kolom yang mengandung 1 utama mempunyai nol ditempat

     lain.

CONTOH
x+2y+4z=16(I)
3x+y-z=4(II)
2x+3y+z=10(III)



 

Prosedur 1 [gantikan a21 dan a31 dengan 0] :

{-3 (I)+II} & {-2(I)+III}. Dan diperoleh :



 

Prosedur 2 [kalikan III dengan -1 ; tukarkan baris II ke III & baris III ke II, alasan: merubah -1 menjadi 1 lebih mudah dibanding merubah -5 menjadi 1]. Hasilnya :



 

Prosedur 3 [gantikan a32 dan a 12 dengan 0] : {5(II)+III} & {-2(II)+I}. Dan diperoleh :

 

Prosedur 4 [gantikan a33 dengan 1] : {1/22 (III)}. Memperoleh hasil :



 

Prosedur 5 [gantikan a13 dengan 0] : {10(III)+I} . Diperoleh hasil :



              



 

Prosedur 6 [gantikan 7 dengan 0] : {-7(III)+II}.




 

Sehingga nilai x = 2, y = 1 dan z = 3.



INTREPOLASI

Pada analisis regresi, kurve atau fungsi yang dibuat digunakan untuk mempresentasikan suatu rangkaian titik data dalam koordinat x-y. Kurve atau garis lurus yang terbentuk tidak melalui semua titik data akan tetapi hanya kecenderungan (trend) saja dari sebaran data, sedang pada interpolasi dicari suatu nilai yang berada diantara beberapa titik data yang telah diketahui nilainya. Untuk dapat memperkirakan nilai tersebut, pertama kali dibuat suatu fungsi atau persamaan yang melalui titik-titik data, setelah persamaan garis atau kurve terbentuk, kemudian dihitung nilai fungsi yang berada di antara titik-titik data.

Pada Gambar 6.1, menunjukkan sket kurve yang dibuat dari data yang sama dengan cara regresi (Gambar 6.1a) dan interpolasi (Gambar 6.1b dan Gambar 6.1c). Kurve pada Gambar 6.1a, tidak melalui semua titik pengukuran, tetapi hanya mengikuti trend dari data menurut garis lurus. Gambar 6.1b, menggunakan segmen garis lurus atau interpolasi linier untuk menghubungkan titik-titik data, sedang Gambar 6.1c, menggunakan kurve untuk menghubungkan titik-titik data.

Metode interpolasi yang sering digunakan adalah interpolasi polinomial. Persamaan polinomial adalah persamaan aljabar yang hanya mengandung jumlah dari variabel x berpangkat bilangan bulat (integer).

CONTOH SOAL:

-2x3+7x5=12 …….(i)

2x1+4x2-10x3+6x4+12x5=28…….(ii)

2x1+4x2-5x3+6x4-5x5=-1…….(iii)

-2x3+0x4+7x5+0x1+0x2       =12 …….(i)

-10x3+6x4+12x5+2x1+4x2  =28…….(ii)

-5x3+6x4-5x5+2x1+4x2        =-1…….(iii)

0x3+0x4+0x5+0x1+0x2       =0……..(iv)

0x3+0x4+0x5+0x1+0x2       =0……..(v)

          a1   a2  a3  a4  a5    b

R1       -2    0  7     0    0     12           

 R2    -10   6  12   2    4     28        R2- 5R1

            R3      -5    6   -5   2   4      -1         R3-5/2R1

 R4      0    0   0    0   0      0

  R5     0    0   0     0   0      0

R2- 5R1

·         -10-5(-2)=0

·         6-5(0)=6

·         12-5(7)=12-35à-23

·         2-5(0)=2

·         4-5(0)=4

·         28-5(12)=28-60à-32

R3-5/2R1

·         -5-5/2(-2)=0

·         6-5/2(0)=6

·         -5-5/2(7)=-5-35/2à-45/2

·         2-5/2(0)=2

·         4-5/2(0)=4

·         -1-5/2(12)=-1-30à-31

          a1   a2  a3  a4  a5    b

R1       -2   0  7       0   0     12          

 R2      0    6  -23   2    4     -32       

            R3      0    6  -45/2   2   4      -31         R3-R2

 R4      0    0   0     0   0      0

  R5     0    0   0     0   0      0

v  R3-R2

·         6-6=0

·         -45/2 – (-23)=(-45+46)/2à1/2

·         2-2=0

·         4-4=0

·         -31-(-32)=1

          a1   a2  a3  a4  a5    b

R1       -2   0  7       0   0     12          

 R2      0    6  -23   2    4     -32     

            R3      0    0  1/2     0    0      1        

 R4      0    0   0     0   0      0

  R5     0    0   0     0   0      0

           x3  x4  x5  x1  x2    b

0x3+0x4+1/2x5+0x1+0x2=1

·         1/2x5=1

·         x5=2

0x3+6x4-23x5+2x1+4x2=-32

·         6x4-23(2)=-32

·         6x4=-32+46

·         x4=7/3

-2x3+0x4+7x5+0x1+0x2=12

·         -2x3+7x5=12

·         -2x3+7(2)=12

·         -2x3=12-14

·         -2x3=-2

·         x3=1

x1=0,   x2=0,  x3=1,   x4=7/3,    x5=2

-2x3+7x5=12 …….(i)

·         -2(1)+7(2)=12

·         -2+14=12

v  2x1+4x2-10x3+6x4+12x5=28…….(ii)

·         2(0)+4(0)-10(1)+6(7/3)+12(2)=28

·         -10+14+24=28

·         4+24=28

v  2x1+4x2-5x3+6x4-5x5=-1…….(iii)

·         2(0)+4(0)-5(1)+6(7/3)-5(2)=-1

·         -5+14-10=-1

·         9-10=-1

4)      2x1+x2+3x3   =11 …….(i)

4x1+3x2+10x3 =28…….(ii)

2x1+4x2+17x3    =31…….(iii)

          a1   a2  a3       b

R1       2    1  3       11          

 R2      4     3  10     28        R2- 2R1

            R3      2     4   17     31         R3-R1

v  R2- 2R1

·         4-2(2)=0

·         3-2(1)=1

·         10-2(3)=4

·         28-2(11)=6

v  R3- R1

·         2-2=0

·         4-1=3

·         17-3=14

·         31-11=20

          a1   a2  a3       b

R1       2     1   3       11          

 R2      0     1   4       6       

            R3      0     3   14     20         R3-3R2

v  R3-3R2

·         3-3(1)=0

·         14-3(4)=2

·         20-3(6)=2

          a1   a2  a3       b

R1       2     1   3       11          

 R2      0     1   4       6       

            R3      0     0   2       2        

           x1  x2  x3    b

v   0x1+0x2+2x3=2

·         2x3=2

·         x3=1

v   0x1+1x2+4x3=6

·         x2+4(1)=6

·         x2=6-4

·         x2=2

v   2x1+1x2+3x3=11

·         2x1+2+3(1)=11

·         2x1=11-2-3

·         2x1=6

·         x1=3

x1=3,   x2=2,  x3=1

v  2x1+x2+3x3   =11 …….(i)

·         2(3)+2+3(1)=11

·         6+2+3=11

v  4x1+3x2+10x3 =28…….(ii)

·         4(3)+3(2)+10(1)=28

·         12+6+10=28

v  2x1+4x2+17x3    =31…….(iii)

·         2(3)+4(2)+17(1)=31

·         6+8+17=31